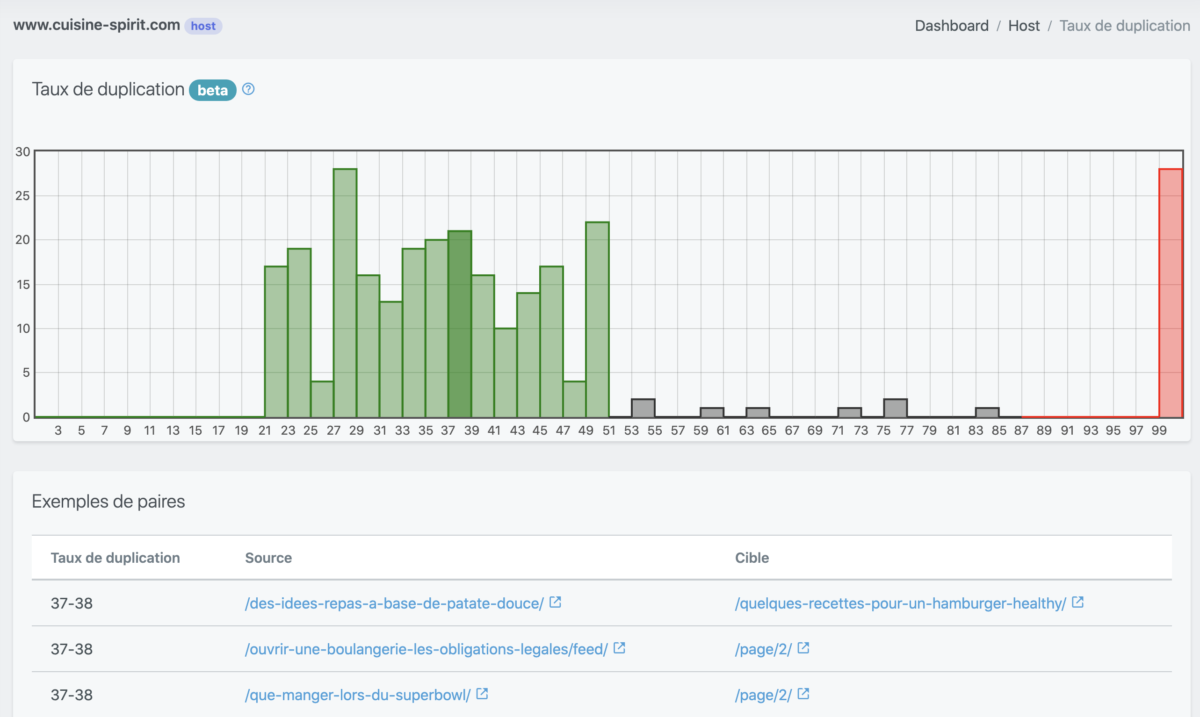
Nous avons récemment introduit dans Babbar la possibilité de calculer la distribution de la duplication interne à un site. Alors vous vous posez sans doute la question de savoir comment marche le calcul de ces near-duplicates ? Notre CTO Guillaume Pitel répond ici à votre question.
Tout part du contenu de chaque page
Le premier élément à considérer dans le calcul de la duplication, c’est le contenu. Pour extraire le contenu d’une page, nous utilisons la même méthodologie que pour les vecteurs sémantiques qui nous servent à calculer les sites et les domaines sémantiquement similaires. A savoir : on garde tout (nous avons beaucoup testé les méthodes d’extraction du contenu core, mais le gain ne semble pas du tout évident).
On peut ensuite appliquer différentes méthodes de normalisation sur le contenu (passage en minuscules, suppression des accents, etc.). Mais en pratique, ce que nous ferons dépendra beaucoup du cas d’usage final. Dans le cas de la duplication interne, on veut souvent détecter non pas des plagiats mais plus des contenus identiques servis dans des contextes différents, donc la normalisation est moins importante. Par ailleurs la normalisation nécessite des travaux spécifiques selon la langue.
La notion de signature
Conserver le texte complet pour calculer la duplication étant hors de question, différentes méthodes de représentation compressée ont été proposées pour aller vite en conservant un minimum de données. On appelle ces représentations des empreintes ou signatures.
MinHash
Une de ces méthodes est par exemple implémentée dans l’outil « simhash » disponible sur plusieurs distributions GNU/Linux (attention à la confusion liée au nom de l’outil), et utilise le principe proposé par Mark Manasse [1].
Ce principe est une variante de la technique du MinHash appliquée sur des « shingles ». Pour comprendre le principe de cet algorithme, imaginons d’abord qu’on découpe un document en mots.
Le principe de base du MinHash est le suivant : pour créer la signature d’un document, on applique une fonction de hachage à chacun des mots qui le compose. Cette fonction de hachage renvoie un nombre.
La signature conservée est le plus petit hachage observé sur un document. Deux documents qui contiennent le mot qui produit le plus petit hachage (et qui ne contiennent pas de mot qui produit un hachage encore plus petit) auront donc le même MinHash.
En pratique, avoir une seule valeur basée sur le hachage d’un seul mot est trop fragile, on peut utiliser deux variantes :
- soit on utilise plusieurs fonctions de hachage indépendantes,
- soit on garde les K plus petits hachages observés pour un document.
La technique utilisée dans l’outil « simhash » correspond à la deuxième méthode, avec K=128 par défaut.
Cet outil génère par défaut des signatures de 128 * 32 = 4096 bits, soit 512 octets. En réalité, les hachages étant « tassés » vers le bas, on peut les exprimer asser facilement de manière compressée, et on peut faire un algorithme de calcul de distance entre les signatures qui soit assez efficace. Ce calcul consiste simplement en une distance de Jaccard (1 – le nombre de hachages identiques/nombre de hachage conservés)
Petit point sur les avantages et les inconvénients de cette approche : 1/ il suffit de rajouter un peu de vocabulaire (par exemple en rajoutant quelques typos par-ci par-là), et la distance augmente vite, car c’est uniquement le vocabulaire qui compte : le fait qu’un mot apparaisse souvent ou pas n’a pas d’importance. 2/ calculer les distances entre de nombreuses signatures est très coûteux en temps.
Le « shingling » vient modérer un peu ces inconvénients : plutôt que de découper un document en mots et donc d’avoir une grosse distortion de distribution entre les mots fréquents et le mots rares, on va le découper en séquences de N lettres, en faisant une fenêtre glissante sur le texte. L’avantage c’est qu’en prenant une taille fixe à la fenêtre, le biais de fréquence sur les mots courts (typiquement les mots grammaticaux) est beaucoup moins présent. En contrepartie, il y a beaucoup plus de tokens à hacher pour calculer la signature, puisque le nombre de shingles = le nombre de lettres du document (à un epsilon près).
SimHash
L’algorithme proposé en 2003 par Moses Charikar de chez Google [2] permet de conserver l’information sur la distribution statistique des mots ou shingles dans le document, l’idée est la suivante :
- Chaque token est haché. Le résultat du hachage est ensuite considéré du point de vue de sa représentation binaire, et convertie en une séquence de 0 et de 1.
ex : un shingle de 8 lettres « SEO made » produit le hachage 0x8ABB, ce qui donne la séquence {1,0,0,0,1,0,1,0,1,0,1,1,1,0,1,1} - Les zéros sont ensuite convertis en -1
- La séquence est sommée à une séquence globale d’entiers qui va représenter la « pré-signature » de notre document.
- Une fois tous les tokens du document traité, on a vecteur dans lequel on a additionné tous les vecteurs de token, par exemple : {-12,67,1,-95,12,3,8,0,-11, ….}
- La signature finale est obtenue en convertissant chacune des valeur en 0 ou 1 selon qu’elle est négative ou positive, on obtient donc : {0,1,1,0,1,1,1,1,0,…….}
Pour calculer la distance entre deux documents, il suffit alors de prendre leurs signature respective et de calculer la distance de Hamming, soit l’opération (très rapide) bitcount(a XOR b).
Dans l’implémentation faite sur Babbar, nous avons amélioré certains aspects pour gagner en performance, et réduire l’impact des tokens trop fréquents. Même si le principe est légèrement différent, le résultat est globalement très proche de la méthode de Charikar qui est citée dans le papier de Google de 2007 [3].
Calcul de la distribution
Pour le calcul de la distribution, c’est-à-dire la représentation qui est proposée par Babbar, on extrait un échantillon de signatures pour un site ou un domaine, et on calcule la matrice des distances. Cette matrice est ensuite fournie de manière synthétique via un histogramme.
[1] Mark Manasse. Finding similar things quickly in large collections. MSR Silicon Valley, 2003.
[2] M.Charikar. Similarity estimation techniques from rounding algorithms. In Proc. 34th Annual Symposium on Theory of Computing (STOC2002).
https://www.cs.princeton.edu/courses/archive/spring04/cos598B/bib/CharikarEstim.pdf
[3] Gurmeet Singh Manku, Arvind Jain, and Anish Das Sarma. 2007. Detecting near-duplicates for web crawling.
In Proceedings of the 16th international conference on World Wide Web (WWW ’07).
http://static.googleusercontent.com/media/research.google.com/en//pubs/archive/33026.pdf